2021上半年中职数学学科知识与能力教师资格证笔试真题及答案
医教及事业单位公考 / 教师从业 / 教师资格证
作者:91搜课网
2022-06-16 09:30

一、单项选择题
1.以下命题不正确的选项是〔 〕
A.有理数集对于乘法运算封闭
B.有理数可以比拟大小
C.有理数集是实数集的子集
D.有理数集不是复数集的子集
参考答案:D
参考解析:一个有理数乘另一个有理数的积仍然是有理数,即有理数对于乘法运算是封闭的,A项正确。有理数与数轴上的点构成单射,任何两个有理数都可以比拟大小,B项正确。实数集包括有理数集和无理数集,而实数集又是复数集的真子集,所以有理数集是实数集的子集,也是复数集的子集,故C项正确,D项错误。
2.设a,b为非零向量,以下命题正确的选项是〔 〕 (1)a×b垂直于a;(2)a×b垂直于b;(3)a×b平行于a;(4)a×b平行于b。 正确的个数是〔 〕
A.0个
B.1个
C.2个
D. 3个
参考答案:C
参考解析:此题考察向量积的知识。向量积的定义,设向量c由向量a与b按如下方式确定:①向量c的模|c|=|a||b| sinθ,θ为向量a与b的夹角;②向量c的方向既垂直于向量a,又垂直于向量b,且其指向符合右手定那么,那么向量c叫作向量a与b的向量积,记作c=a×b。根据向量积的定义,可知题干中的(1)(2)正确,(3)(4)错误。故此题选C。
3.设ƒ(x)为开区间(a,b)上的可导函数,那么以下命题正确的选项是〔 〕
A.ƒ(x)在(a,b)上必有最大值
B.ƒ(x)在(a,b)上必一致连续
C.ƒ(x)在(a,b)上必有界
D.ƒ(x)在(a,b)上必连续
参考答案:D
参考解析:根据微积分的知识,可导的函数必连续所以D项正确。
4.边长为4的正方体木块,各面均涂成红色,将其锯成64个边长为1的小正方体,并将它们搅匀混在一起,随机抽取一个小正方体,恰有两面为红色的概率是( )
A.3/8
B.1/8
C.9/16
D.3/16
参考答案:A
参考解析:锯成64个边长为1的小正方体后,涂色的面有以下几种情况:涂3面的小正方体分别在大正方体的8个顶点处,共有8个;涂2面的小正方体分别是大正方体的每条棱的中间的2个,而大正方体共有12条棱,那么,涂2面的小正方体有2×12=24个;涂1面的小正方体分别是每个面的中间的4个,而大正方体共有6个面,那么,涂1面的小正方体有4×6=24个;6个面都没有涂色的小正方体有64-8-24-24=8个,则随机抽取一个小正方体,恰有两面为红色的概率是24/64=3/8.
5.在空间直角坐标系中,抛物柱面y2=2x与平面x-y-2=0的交为( )
A.椭圆
B.两条平行直线
C.抛物线
D.双曲线
参考答案:B
参考解析:抛物柱面y2=2x与平面x-y-2=0可看作是xOy平面内的曲线y2=2x与直线x-y-2=0沿平行。轴方向平移得到的面。联立方程y2=2x与方程x-y-2=0,消去y得x2-6x+4=0, 其中△=62-4×4×1=20>0,故在zOy片面内曲线y2=2x与直线x-y-2=0的交是两个点。沿着平行于2轴的方向平移这两个点,就得到了两条平行直线,即抛物柱面y2=2x与平面x-y-2=0的交为平行于z轴的两条平行直线。
6.下面不属于“尺规作图三大问题”的是( )
A.三等分任意角
B.作一个立方体使之体积等于已知立方体体积的二倍
C.作一个正方形使之面积等于已知圆的面积
D.作一个正方形使之面积等于已知正方形面积的二倍
参考答案:D
参考解析:“尺规作图三大问题”是指三等分角,即三等分任意角;立方倍积,即作一个立方体使之体积等于已知立方体体积的二倍;化圆为方,即作一个正方形使之面积等于已知圆的谣积。
7.下列内容属于高中数学必修课程内容的是( )
A.风险与决策
B.平面向量
C.数列与差分
D.矩阵与变换
参考答案:B
参考解析:平面向量是高中数学必修4的内容,风险与决策是高中数学选修4—9的内容,数列与差分是高中数学选修4—3的内容,矩阵与变换是选修4—2的内容
二、简答题
1.简述确定中学数学教学方法的依据。
参考解析:
教学方法是教师引导学生掌握知识、技能,获得身心发展而共同活动的方法。选择中学数学教学方法的依据:(1)依据教学的目的和任务选择教学方法;(2)根据教材内容的特点选择教学方法;(3)依据学生的实际情况选择教学方法;(4)依据教师本身的素质选择教学方法;(5)依据各种教学方法的职能、适用范围和使用条件选择教学方法;(6)依据教学时间和效率的要求选择教学方法。
2.简述你对《普通高中数学课程标准》(实验)中“探索并掌握两点间的距离公式”这一目标的理解。
参考解析:
“探索”是过程与方法目标行为动词,“掌握”是知识与技能目标行为动词。“探索和掌握两点间距离公式”这一目标的设置,要求学生不仅要记住该公式的内容,还需要掌握该公式的推导过程,联系知识问的内在关系,体会其中的数学思想,为进一步的学习提供必要的数学准备。
探索并掌握两点间的距离公式有助于学生认识数学内容之间的内在联系。两点间的距离公式是中学数学学习的主要内容之一,在高中数学中占有重要地位。探索两点间的距离公式的过程中需要数轴、直角坐标系、直角三角形、勾股定理等知识,而两点间的距离公式又是几何中最简单的一种距离,点到直线的距离、两条平行直线间的距离、两平行平面间的距离、异面直线公垂线段的长度等计算最终都可以归结为两点间的距离。学生经历探索并掌握两点间的距离公式的学习过程,能够更好地体会并理解这些知识点的内在联系,这对学生构建知识体系,增强学习数学的信心很有帮助。
探索并掌握两点间的距离公式有助于学生体会数形结合思想,形成正确的数学观。探索两点间的距离公式经历将几何问题代数化的过程,用代数的语言描述几何要素及其关系。两点问的距离公式是将几何问题转化为代数问题的重要桥梁和工具。利用距离公式分析代数结果的几何意义,也有助于最终解决几何问题。引导学生经历这样的数形结合的过程,对发展学生的推理能力很有益处。
三、解答题
设f(x)是R上的可导函数,且f(x)>0。若f'(x)-3x---2f(x)=0,且f(0)=1,求f(x)。
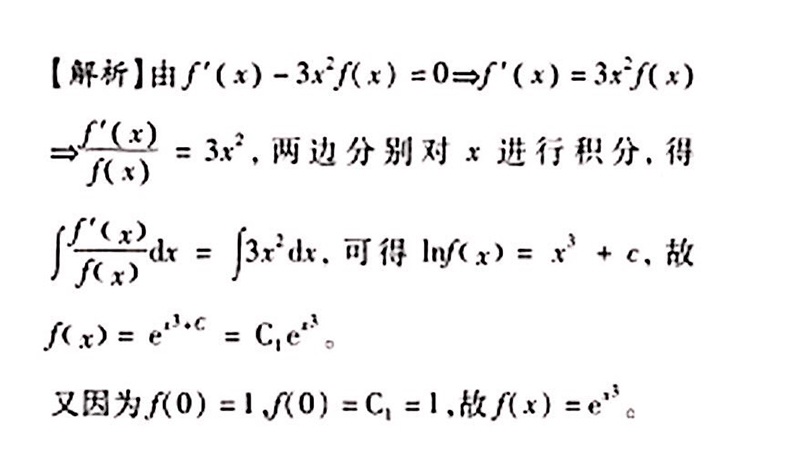
四、论述题
论述在高中数学教学中如何理解与处理好面向全体学生与关注学生个体差异的关系。
参考解析:
教学活动应努力使全体学生达到课程目标的基本要求,同时要关注学生的个体差异,促进每个学生在原有基础上的发展。
①对于学习有困难的学生,教师要给予及时的关注与帮助,鼓励他们主动参与数学学习活动,并尝试用自己的方式解决问题、发表自己的看法;要及时地肯定他们的点滴进步,耐心地引导他们分析产生困难或错误的原因,并鼓励他们自己去改正,从而增强学习数学的兴趣和信心。对于学有余力并对数学有兴趣的学生,教师要为他们提供足够的材料和思维空间,指导他们阅读,发展他们的数学才能。
在教学活动中,要鼓励与提倡解决问题策略的多样化,恰当评价学生在解决问题过程中所表现出的不同水平。问题情境的设计、教学过程的展开、练习的安排等要尽可能地让所有学生都能主动参与,提出各自解决问题的策略。引导学生通过与他人的交流选择合适的策略,丰富数学活动的经验,提高思维水平。
赞同





